Skip to main content
The challenge with hedging impermanent loss is its nonlinearity and convexity. Spot positions and perpetual futures move linearly with price—they gain or lose value in direct proportion to price changes. Impermanent loss, by contrast, is convex: the loss accelerates as price moves further from the entry point. This mismatch means linear instruments alone cannot neutralize IL. We need an instrument that also has convexity—one that gains value at an accelerating rate as price moves in either direction. Options provide exactly this property. For a symmetric LP range, a straddle position (buying both an at-the-money put and an at-the-money call) creates a payoff profile that mirrors the shape of impermanent loss. As price moves away from the strike in either direction, the straddle gains value, offsetting the IL incurred by the LP position. Combined PnL Figure: Combined PnL of LP + Short + Straddle When we combine all three components—the LP position, the short perpetual hedge, and the straddle—the resulting portfolio has a flattened PnL profile across a wide range of prices. The position captures fee revenue while neutralizing both directional exposure (via the short) and impermanent loss (via the straddle). Unlike a portfolio with only a short hedge, this fully hedged position does not suffer losses when price moves to the range boundaries. The options payoff compensates for the IL that the linear short cannot cover.

​
Selecting Option Maturity

However, introducing options requires us to specify a maturity date, which brings us to the next consideration. To determine the appropriate option tenor, we estimate how long the LP position is expected to remain in range. If price exits the range, the LP position stops earning fees and must be closed or repositioned. Assuming the underlying asset follows a driftless geometric Brownian motion (GBM), we can derive the expected time to reach a given price boundary. For a return level rr (the distance to the range boundary as a percentage), the expected time is: T=[ln⁡(1+r)]2σ2T = \frac{[\ln(1+r)]^2}{\sigma^2} where σ\sigma is annualized volatility. Example: ETH volatility = 60%, price range = ±20% T=[ln⁡(1.2)]20.62=0.03320.36≈0.092 years≈34 daysT = \frac{[\ln(1.2)]^2}{0.6^2} = \frac{0.0332}{0.36} \approx 0.092 \text{ years} \approx 34 \text{ days} This calculation guides our option maturity selection: we match the option tenor to the expected duration of the LP position. Tighter ranges mean shorter expected durations and therefore shorter-dated options.

​
Evaluating Profitability

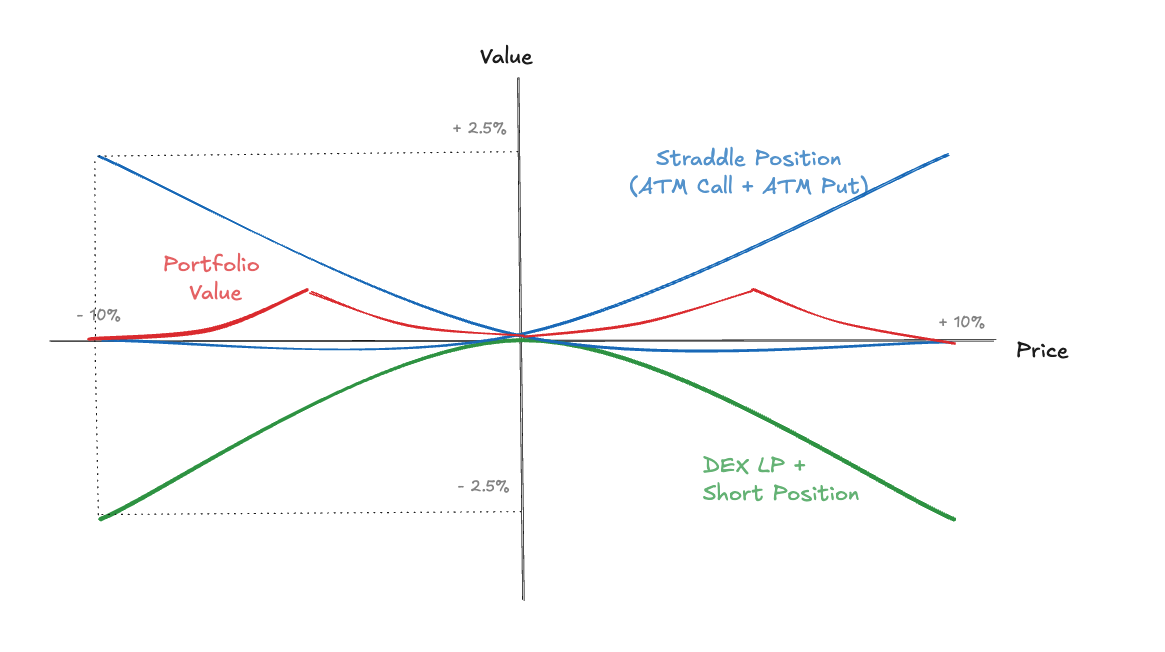
With the hedging framework established, the profitability condition becomes straightforward: LP Fee Revenue+Funding Income>Straddle Premium\text{LP Fee Revenue} + \text{Funding Income} > \text{Straddle Premium} If the fees earned from the LP position plus any funding payments received from the short perpetual exceed the cost of the options hedge, the position is profitable. It’s important to note that adding options does not magically create yield where none exists. If a pool’s fee revenue is fundamentally insufficient relative to the volatility of its underlying assets, the hedge simply reshapes the risk profile without improving the economics. The option premium reflects the expected cost of the volatility exposure we’re hedging away. However, this framework provides two significant benefits:
  1. Variance reduction: By hedging IL, we dramatically reduce the volatility of returns. The position generates more consistent yield across different price paths, rather than being highly profitable in some scenarios and deeply unprofitable in others.
  2. Rigorous evaluation: Using established option pricing models allows us to evaluate opportunities on a sound theoretical basis. Rather than naively selecting pools with the highest displayed APY, we can compare fee revenue against the true cost of the associated risks.